Conical folding surfaces in three steps
It's the time to change the way to think the origami. In our book "ARCHITETTURA DELLE SUPERFICI PIEGATE - le geometrie che muovono gli origami " Graziano Mario Valenti explains the geometrical construction that is behind the conical origami surface. Starting from that explanation, I want to show a digital way for solve the same issue.
In the real word, a cone is a continuous surface, but if we want to represent it with a drawing method, we have to discretize it with curves. The same for the digital method of representation.
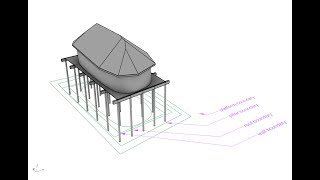
My aim is to draw the origami in the picture. it is possible by doing three steps.
1 - Create the physical model
Do it with paper! It is the unique manner to understand the behavior of the fold joined to the material of the paper. So, looking the pattern we can see that It is composed by three faces. During the movement, two faces keep their planar condition, the other curves itself to become a cone. To simulate the movement into a digital environment, I decided to use a physical engine inside Grasshopper: Kangaroo 2.0.
2 - The right topology
Kangaroo works with mesh, so the problem now is create a correct mesh topology capable to follow the behavior of the paper model.
As you know the cone could be represented by Its generatrices, and if I develop the cone with its generatrices, it becomes a sort of wheel with rays but without a part. The rays suggest me how to tessellate the pattern of the origami, I mean how to discretize the big curved face. So in this case it is useful to create a kind of " hide folds" that don't fold, but they allow the curvature of the face. But that is possible by deciding the inner stresses between faces. Only in this way I can create differences between hinges and line for the curvature of the pattern face.
3 - Forces
The forces that play to allow the movement of the pattern could be split in two groups. The first one is composed by inner forces to constrain the length of the hinges (hidden and not hidden) and forces to constrain the angles between two consecutive small triangles to maintain a rest position of 180°.
There is another group of external forces useful to make the first fold and orient the direction of the movement. The movement is activated with other external forces.
